Regular expressions and finite state automata
Lecture 6
Table of Contents
- Regular expressions
- How would you write this program?
- Example
- Regular expression language
- Matching against regular expressions
- Finite automata
- Turnstile automaton
- Finite state automata are a model of computation
- Chomsky hierarchy
- Chomsky hierarchy table
- Benefits of abstract computational models
- Applications of finite state machines
- Examples from gaming
- Abstract machine model
- Definition of automata
- Graphical representation with state diagrams
- Example: identifiers
- More complex automaton: numbers
- Nondeterministic vs. Deterministic
- Demo: diagrams
- Transition tables
- Demo: transition tables
- In our compiler
- Automate lexing by generating automata
- Convert via subset construction
- Translate each regex in order of operations
- Concatenation
- Alternation
- Kleene closure
- NFA example
- Demo: converting regex to NFA
- Construct DFA from an NFA systematically
- Sketch of the subset construction algorithm
- Demo: converting NFA to DFA
- Conclusion
Regular expressions
String pattern matching
- phone numbers
- email addresses
- programming language tokens
How would you write this program?
- Search for an email address in a text file?
Example
Sequence
- Area code is three digits
Alternation
- A digit is either a 0, 1, 2, .., 9
Parentheses are just used to make order of operations explicit, just like in arithmetic
Repetition
- Any number of characters before the @ sign
Optional elements
- E.g., country code
Wild cards
- Allow any character (or some subset of characters)
Regular expression language
- concatenation, e.g.,
ab - alternation, e.g.,
a|b - Kleene closure, e.g.,
a*
The order of operations, from highest to lowest, is Kleene closure, concatenation, and alternation.
One way to remember order of operations, is that alternation is like addition or logical or, concatenation is like multiplication or logical and, and Kleene closure is like exponentiation.
Regular expressions in practice
- Lots of syntactic sugar available
- python library (perl syntax)
Matching against regular expressions
- Given an expression (ab|d)*
- Can hand-write a program for specific regular expression
- But we can also automate their generation
Finite automata
- States and transitions between states
- Example: turnstile

By N/D - Link CC BY-SA 4.0, https://commons.wikimedia.org/w/index.php?curid=131513928
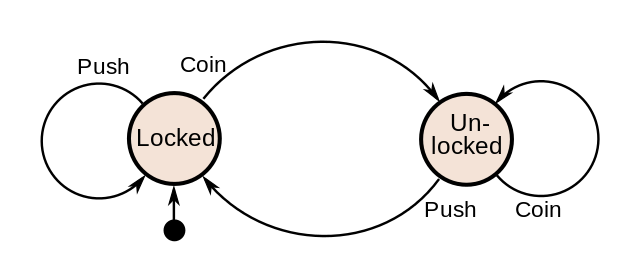
Turnstile automaton
- Turnstile states: locked and unlocked
- Turnstile transitions: push and coin
- Transition move from state to state
- E.g., coin causes unlock, push reutrns to locked
By Chetvorno - Link - Own work, CC0, https://commons.wikimedia.org/w/index.php?curid=20269475
Finite state automata are a model of computation
- Corresponds to regular languages
- Any regular expression can be recognized by a finite automaton and vice-versa
- AKA
- Finite state machines, Finite automaton, State machine
Here's our first abstract machine model
Takeaway here: if we can frame the problem we want to solve as a finite statement machine, then we already have a language, regular expressions, to write a solution in.
Instead of trying to create a de novo algorithm, we can map the problem into the abstract problem of finite state transitions or regular language pattern matching.
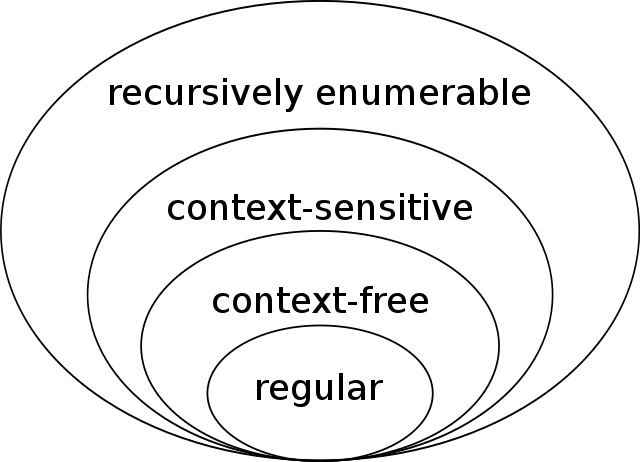
Chomsky hierarchy
By J. Finkelstein - Own work, CC BY-SA 3.0, https://commons.wikimedia.org/w/index.php?curid=9405226
Chomsky hierarchy table
Equivalence between language and computation
| Language | Computation |
|---|---|
| Regular | Finite automata, regex |
| Context-free | Parsers, push-down automata (PDA) |
| Context-sensitive | Parsers, non-deterministic PDAs |
| Recursively enumerable | Turing machine |
- Regular languages
- finite automata, regular expressions
- Context-free languages
- Syntactic structures Parsers, push-down automata
- Context-sensitive
- Syntax depends on surrounding contet
- (Fancier) parsers, non-deterministic push-down automata
- Recursively enumerable
- Recognized by a Turing machine
Benefits of abstract computational models
- Matching regular expressions is solved
- Map your problem to a regular expression
- Use an existing tool to compute solutions for you
Researchers have spent time automation the solution to this abstract problem, so that you don't have to repeat it.
Just like a compiler takes a programming language and translates it to assembly, a regular expression.
Then you can frame your problem as a regular expression, write it, and a regular expression compiler will turn this into code for you.
Applications of finite state machines
- Traffic lights
- Turnstiles
- Vending machines
- Lexers
String pattern matching is equivalent to many automation tasks
Examples from gaming
Abstract machine model
- Formal language: potentially infinite set of strings
- Each string drawn from a finite alphabet
- Each string element itself is finite
Definition of automata
- Finite alphabet of symbols (like regular languages)
- Finite set of states
- State transition function
- Initial state and final state(s)
Graphical representation with state diagrams
- States: circles
- Transitions: labeled arrows
- Starting state: in-arrow
- Accepting states: doubled circles
Example: identifiers
- Letters and digits are character classes
- Makes drawing easier
- "other" is all characters besides lettersdigits
- Represents teh decision based on a lookahead
- Matches longest identifier sequence

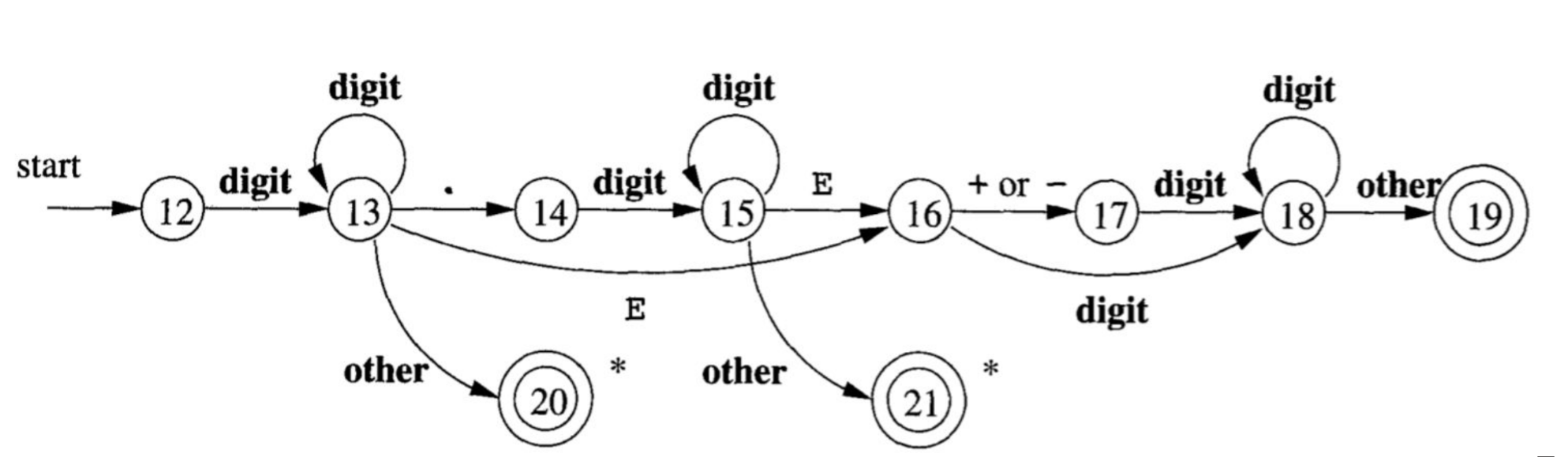
More complex automaton: numbers
- What kinds of numbers can be represented here?
- What is an equivalent regular expression?
Nondeterministic vs. Deterministic
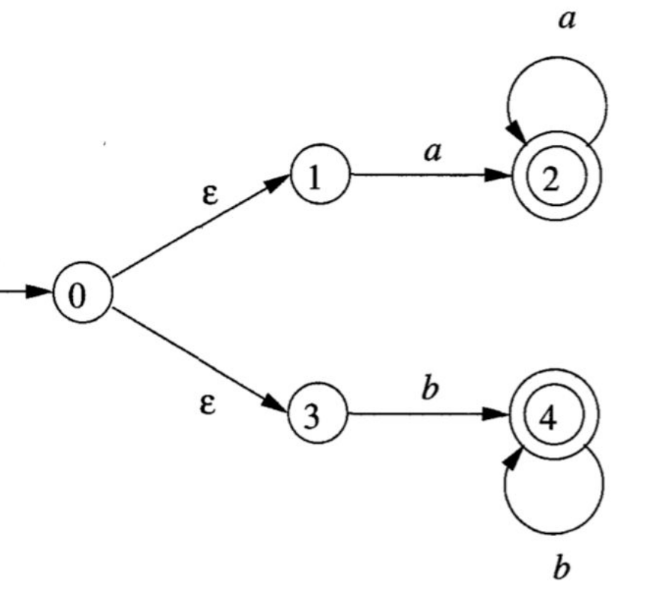
- Deterministic: one state at a time
- Nondeterministic: mulitples states at once
- Same symbol, multiple transitions
- Epsilon (empty string) transitions
Examples
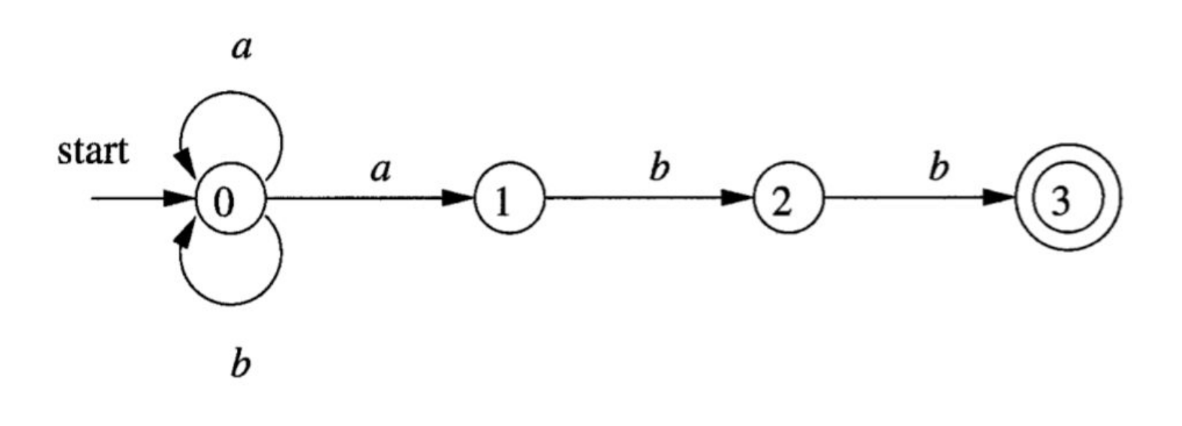
Demo: diagrams
- L(L|D)*
- (a|b)*abb
- aa*|bb*
(a|b)*abb
motivate using NFAs and \(\epsilon\) to make it easier to try multiple possibilities
attempt to construct intuitively, then see systematic method next
Transition tables
- Can use table instead of diagram
- Convenient for implementation
- DFAs vs. NFAs
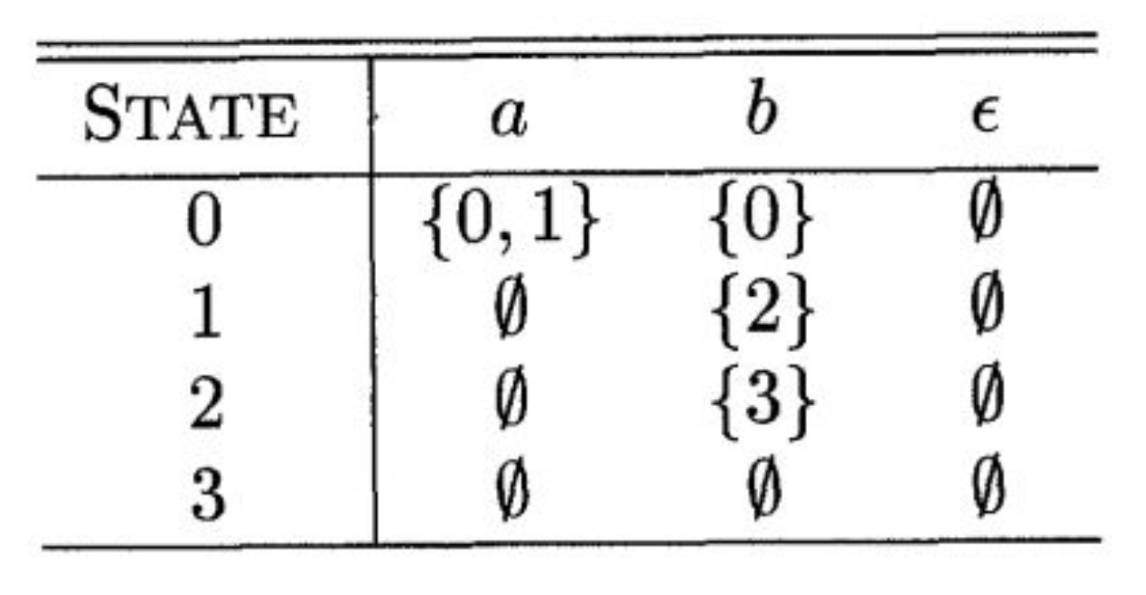
Demo: transition tables
- L(L|D)*
- (a|b)*abb
- aa*|bb*
do a table driven version of (a|b)(a|b)*
one column per letter of the alphabet
one row per state
In our compiler
- Use finite state machines to automate lexing
- One regular expression per token
- flex compiles regular expressions to a C program
- Output recognizes tokens matching the regular expressions
Automate lexing by generating automata
- Specific tokens via regular expressions
- Existing algorithm to convert regx to automata
- This is what flex does
- Two methods
- Simulate an NFA
- Convert an NFA to a DFA (subset construction)
Convert via subset construction
- NFA can be multiple states at once
- Finite automata means finite number
- Key observation: there are finite number of combinations of NFA states
- How many subsets of states are there in a finite set?
The powerset tell us how many combinations of finite states that are possible.
Translate each regex in order of operations
- Convert each subexpression to an NFA
- Combine NFAs for each subexpression
- Each regex operation corresponds to an NFA template
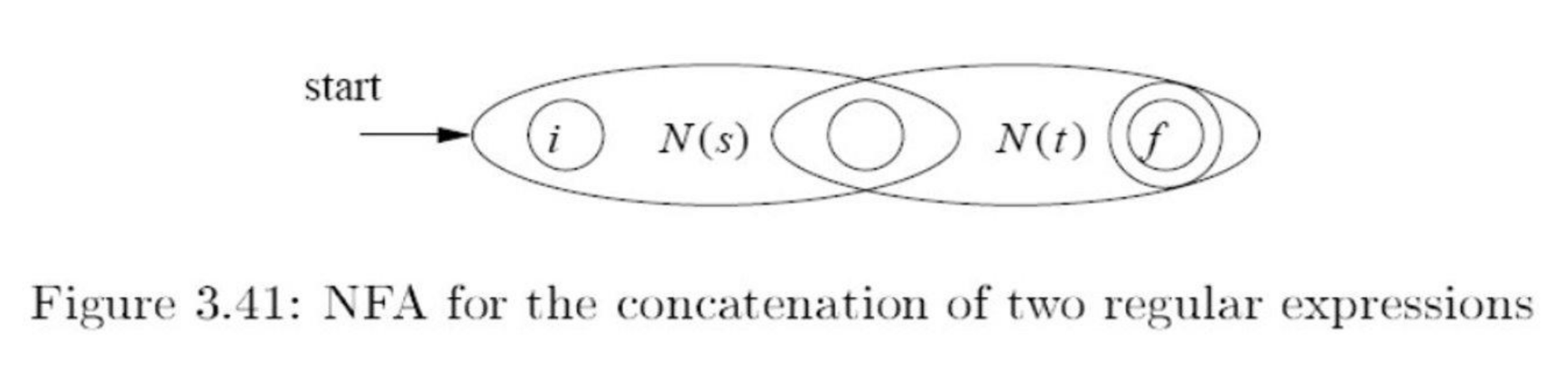
- Concatenation
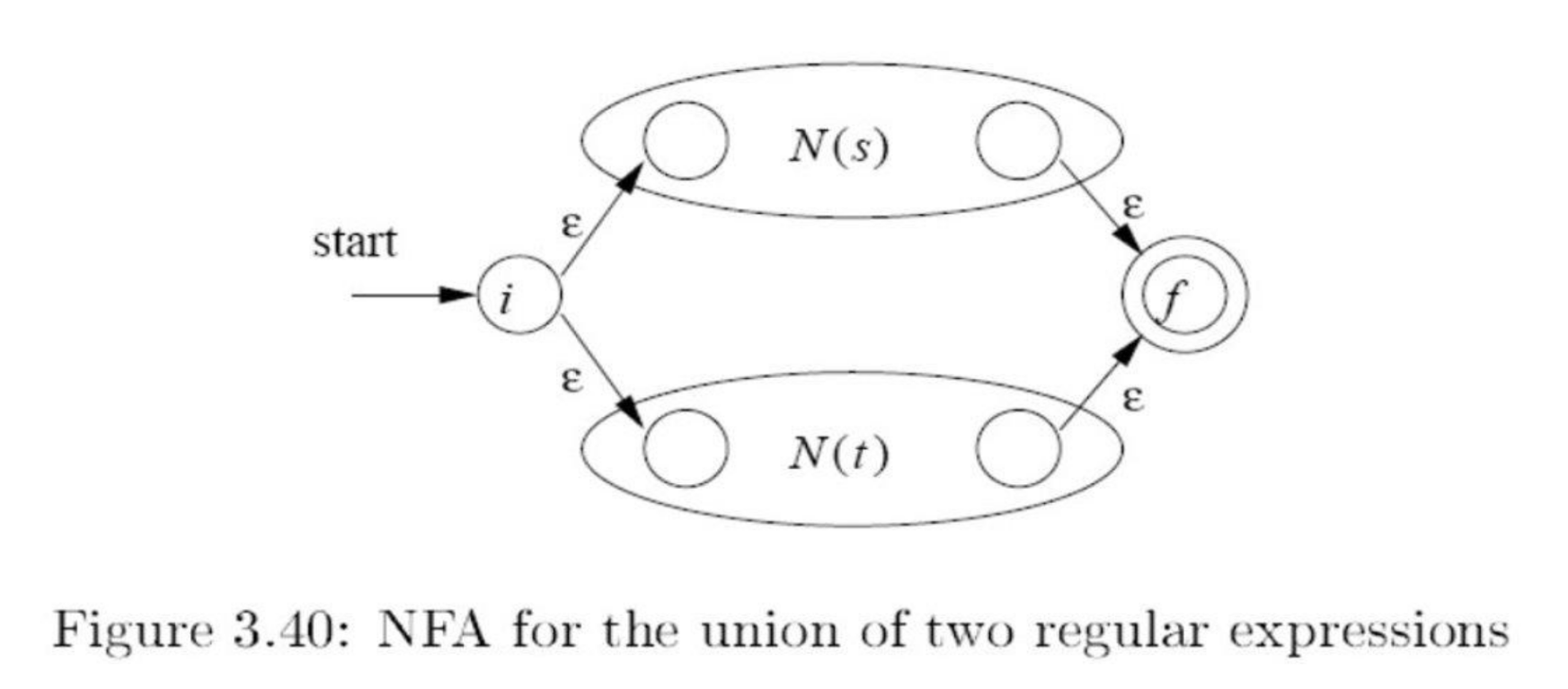
- Alternation
- Kleene closure
Concatenation
Alternation
Kleene closure
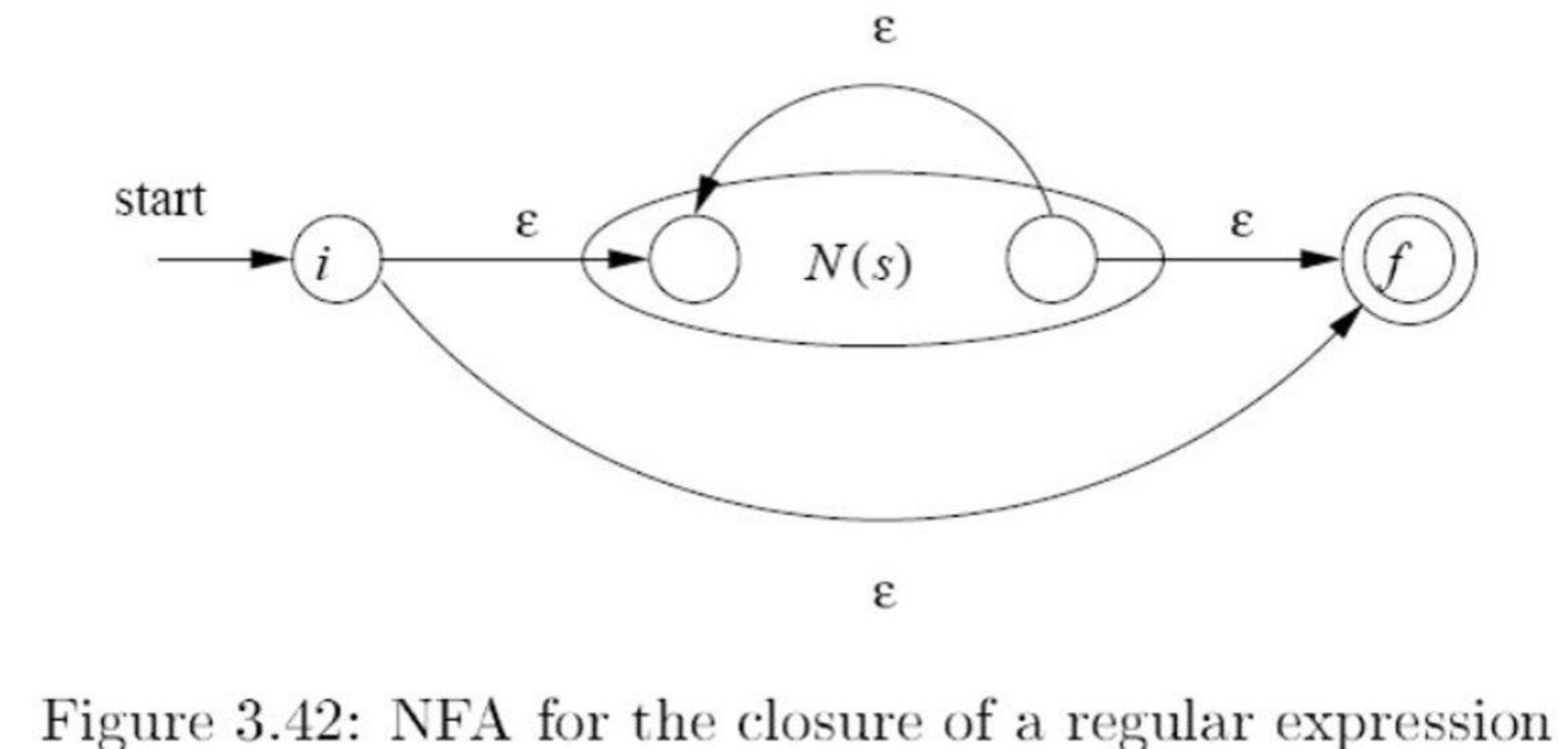
NFA example
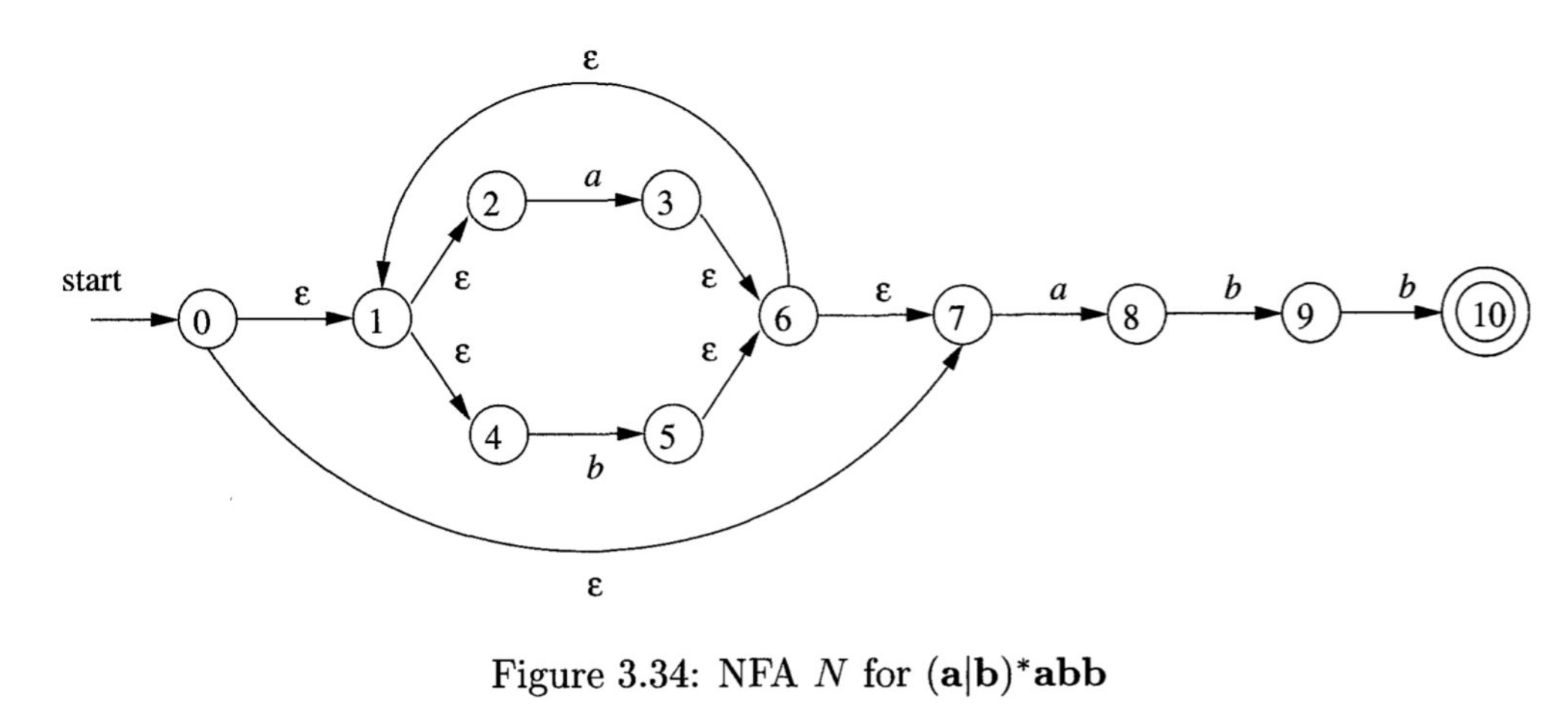
Demo: converting regex to NFA
- (a|b)*abb
- aa*|bb*
- ((a|bc)b)*
(a | b)*abb
much easier with NFAs
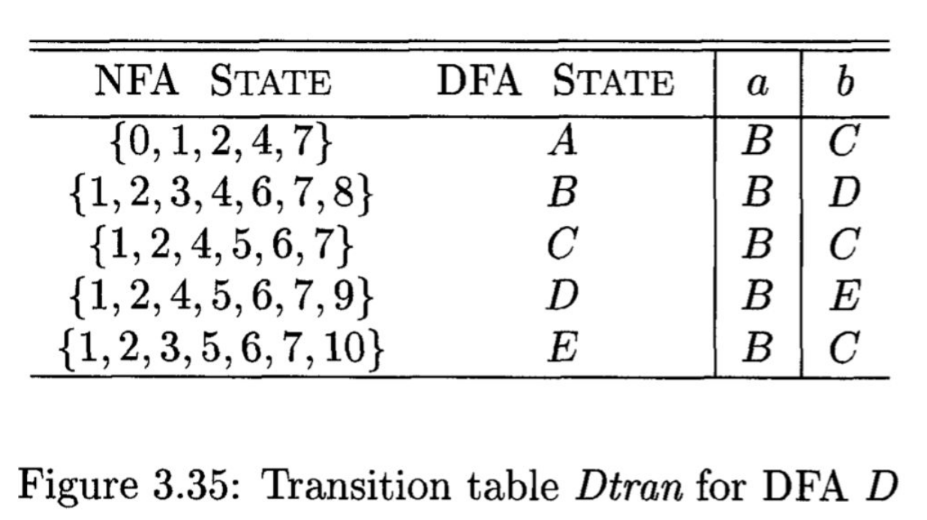
Construct DFA from an NFA systematically
- Each DFA state created from subset of NFA states
- NFA can be multiple states at once
- "Simulate" being in multiple states using a single state
- The multiple states are a subset of the NFA states
- Create the DFA by calling each subset a single DFA state
Sketch of the subset construction algorithm
- Start at the NFA's starting state
- Group all states reachable by \(\epsilon\) (epsilon)
- This is the $ε$-closure/
- Call this group of the states the initial state
- For each symbol s in the alphabet (which is finite)
- Get all state that s transitions to
- Find the $ε$-closure of those states
- Call this group of states one DFA state
- Repeat for all combinations states and symbols
- Stop when all are covered
Demo: converting NFA to DFA
- (a|b)*abb
- aa*|bb*
- ((a|bc)b)*

Conclusion
- We can automatically generate lexers
- Regular expressions correspond to automata
- Implemented with transitions tables, if statements, etc.
- Simpler to generate NFAs from regular expressions
- Subset construction to convert NFA to DFA
- Alternative: simulate an NFA