

Next: 2.2 Problem
Up: 2 Position
Previous: 2 Position
The vocabulary of our simple
logical formalism is composed of :
-
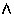 ,
, 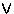 ,
, 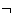 connectors and
connectors and 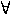 ,
, 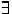 quantification symbols,
quantification symbols,
- a set of logical variables and a set of logical
constants
![[*]](foot_motif.gif) ,
,
- a set of predicates (equality, etc).
The values domain of logical variables and constants is composed of
integers, strings, sets, lists, tables, etc. Before defining logical formulae, we define
terms that compose a logical formula :
- a logical variable is a term (if this variable is referenced under
a quantification symbol),
- if f is a logical constant in n arguments and t1,...,tn
some terms then f(t1,...,tn) is a term.
Definition of logical formula :
- if P is a predicate in n arguments and t1,...,tn some terms
then P(t1,...,tn) is a (atomic) formula,
- if A is a formula then
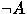 is a formula,
is a formula,
- if A is a formula, t a term and x a logical variable then
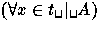 and
and 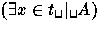 are formulae,
are formulae,
- if A and B are formulae then
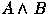 and
and 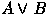 are
formulae.
are
formulae.
We introduce another notation often used in logic and named
the conditional operator. The logical definition of it is :
| 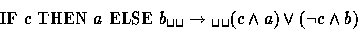 |
(1) |


Next: 2.2 Problem
Up: 2 Position
Previous: 2 Position
Alain Cougoulic
Sept. 2, 1997
![]()
![]()
![]()
![[*]](foot_motif.gif) ,
,