

Next: 2.3 Explicit determinism
Up: 2 Position
Previous: 2.1 A simple logical
The simulation of specifications permits one to finalize
specifications (i.e. to bring them to there final version) or
to validate system implementations with regard to its specifications. We are
interested in finalizing specifications. In the
case of a service call (when an object state switches), the post-condition
related to it references object specification variable values and how
they change during the call execution. Only
post-conditions define these changes because if a pre-condition defines
many value change, then this pre-condition is a post-condition of an other service
call. An example is the couple of pre/post-conditions
[ n<l,n'=n+1 ] defined in section 1, the
post-condition n'=n+1 specifies the change of n value during the addition
of a subscriber to a telephone dispatcher.
When we simulate specifications, we want to animate the object
value changes
on the simulated object states. We classify these value changes in two categories :
- a specification variable takes only one new value,
- a specification variable must choose between some new values.
For example, these two categories of value changes are presented in this post-condition :
| 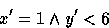 |
(2) |
The x'=1 sub formula defines only one possible new value for x, the
value 1. This sub formula is deterministic. The y'<6 sub formula defines a
set of possible new values for y, this set is {0,1,2,3,4,5}. This
sub formula is non-deterministic. The deterministic notion
is associated with the substitution notion. A substitution is a
set of pairs of variables and values. A substitution e is defined on
a formula f if the set of variables in the substitution e is the
set of variables in the formula f. The definition 1 give a possible definition of
the determinism of a formula.
Definition 645 (1)
Let f be a formula, f is deterministic if :
| 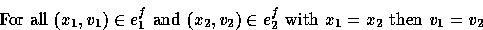 |
(3) |
where eif is a substitution and eif satisfies f![[*]](foot_motif.gif) .
.
From a practical point of view, the treatment of the deterministic part of a
formula is more efficient. If a post-condition is
deterministic then the object related to this post-condition can
only have one state after execution of the service related to this
post-condition. Otherwise the object can be in many different states, and we must
choose between these states, or study all possibilities. In fact, the
main problem discussed in this paper concerns the distinction between the
determinism and the non-determinism of the formula.
To separate the determinism from the non-determinism of a formula seems to be trivial
in formula 2. We can imagine how to define an algorithm that
computes the separation between the
determinism and the non-determinism of a formula. However, our simple
logical formalism defined in subsection 2.1 does not
restrict the set of predicates, in particular, we use some
undecidable predicates, in this case, all algorithms are also
undecidable. An element of solution is the notion of explicit determinism
which we describe in subsection 2.3.


Next: 2.3 Explicit determinism
Up: 2 Position
Previous: 2.1 A simple logical
Alain Cougoulic
Sept. 2, 1997
![]()
![]()
![]()
![[*]](foot_motif.gif) .
.