2.1 Abstract Specification

At the most abstract level, all actions of a system can be assumed to occur in intervals without overlap. An interval at this level of abstraction represents a cycle of the concrete system.

A theory SData gives definitions of the types and constants used in the system, and will be included in each of the other theories:

Types

 
$PState = \{ running, off \}$
$PCState = \{ flow, noflow \}$
$Condition = \{ failed, operating \}$
@$Pump = \{ p1, p2, p3, p4 \}$

Constants

 
$M1: \nat$   /*  Minimum water level */
$M2: \nat$    /*  Maximum water level */
$N1: \nat$    /*  Minimum normal water level */
$N2: \nat$    /*  Maximum normal water level */
$W: \nat_1$    /*  Maximum steam production */
$C: \nat_1$    /*  Capacity of boiler */
$P: \nat_1$    /*  Capacity of pump */
$U1: \nat$    /*  Max rate of steam increase */
$U2: \nat$    /*  Min rate of steam increase */
$\tau: \nat_1$    /*  Sampling interval */

Axioms

$M1 < N1 ~\land ~N1 < N2 ~\land ~N2 < M2$

Each physical component has an associated monitor which provides an interface between it and the controller. This monitor is responsible for managing the protocol of communications between the controller and the components, and for detecting errors in data and communications.

The axioms of the monitor theory for the water measure formalise the requirements given in [2, pages 500-509].

Attributes

 
$water\_measure\_condition: Condition$
$water\_quantity: \num$

Actions

(With write frames presented as sets of attributes:)  
$level(lev: \num)$   $\{ water\_quantity \}$
$water\_measure\_failed$   $\{ water\_measure\_condition \}$
$transmission\_failure$   $\emptyset$
$level\_failure\_detection$    $\emptyset$
$level\_failure\_acknowledgement$    $\emptyset$
$level\_repaired$   $\{ water\_measure\_condition \}$
$level\_repaired\_acknowledgement$    $\emptyset$

Axioms

Initially the water quantity is 0 and the measure is operating:

$$BEG ~\implies~ water\_quantity = 0 ~\land \\ \t2 water\_measure\_condition = operating$$

A water measure failure event occurs if we receive a level(lev) message with lev < 0 or lev > C:

$$\exists lev: \num \cdot level(lev) \land (lev < 0 \lor lev \gt C) ~\implies\\ \t7 water\_measure\_failed$$

A transmission failure occurs if we do not receive a unique level message in the current cycle:

$$\lnot \exists_1 lev: \num \cdot level(lev) ~\implies~~ transmission\_failure$$

Notice that this includes the case where no level message is received.

If a level measure failure occurs, the system must react by recording the failure:

$$water\_measure\_failed ~\implies~ \bigcirc{water\_measure\_condition} = failed$$

The signal $level\_failure\_detection$ must then be repeated until
$level\_failure\_acknowledgement$ is received:

$$water\_measure\_failed ~\implies~ \\ \t1 (level\_failure\_detection ~{\cal U}~level\_failure\_acknowledgement)$$

A $level\_repaired$ signal resets the $water\_measure\_condition$ attribute:

$$\lnot{water\_measure\_failed} \land level\_repaired ~\implies~ \\ \t5 \bigcirc{water\_measure\_condition} = operating$$

and leads to the generation of a $level\_repaired\_acknowledgement$:

$$level\_repaired ~\implies~ level\_repaired\_acknowledgement$$

A valid water level event sets the value of $water\_quantity$:

$$\lnot{water\_measure\_failed} ~\land~\lnot{transmission\_fai... ...\\ \t5 (level(lev) ~\implies~ \bigcirc{water\_quantity} = lev)$$

The theory of the steam measure monitor is identical in structure to the water measure monitor. Formally it is an isomorphic image under the morphism which maps C to W,
$water\_measure\_condition$ to $steam\_measure\_condition$, etc.

A similar structure can be given for the theory of the pump, pump monitor and the pump controller and its monitor. Indeed we can recognise a number of commonalities between the monitor theories (only the criteria for detecting sensor failures, and for recording the current state, are different). There are common subtheories FailureManager of the form

Attributes

 
condition: Condition

Actions

 
$component\_failed$   $\{ condition \}$
$component\_repaired$    $\{ condition \}$
$failure\_detection$   $\emptyset$
$failure\_acknowledgement$   $\emptyset$
$repaired\_acknowledgement$    $\emptyset$

Axioms

$$BEG ~\implies~condition = operating$$

$$component\_failed ~\implies~\bigcirc{condition} = failed$$

$$component\_failed ~\implies~\\ \t4 (failure\_detection~{\cal U}~failure\_acknowledgement)$$

$$\lnot{component\_failed} \land component\_repaired ~\implies~ \bigcirc{condition} = operating$$

$$component\_repaired ~\implies~ repaired\_acknowledgement$$

These in their turn could be subdivided into parts dealing with the communication protocol (axioms 3 and 5) and parts dealing with the recording of failure status (axioms 1, 2 and 4).

A theory Transmission has the form

Actions

 
$component\_state(val: \num)$   $\emptyset$
$transmission\_failure$   $\emptyset$

Axioms

$$\lnot \exists_1 lev: \num \cdot component\_state(lev) ~\implies~~ transmission\_failure$$

where we regard the PState and PCState types as isomorphic to $\{ 0, 1 \}$as in [2].

Therefore the $Water\_Measure\_Monitor$ theory can be re-expressed in terms of Transmission, via the morphism m7 of Figure 2:

$$component\_state(s) ~\mapsto ~ level(s) \\ transmission\_failure ~\mapsto~ transmission\_failure$$

and FailureManager, via the morphism m1

$$condition ~\mapsto~ water\_measure\_condition \\ component\_... ...d\_acknowledgement ~\mapsto ~ level\_repaired\_acknowledgement$$

The attribute $water\_quantity$ and axioms to initialise and set this quantity are defined locally in $Water\_Measure\_Monitor$, and the axiom

$$\exists lev: \num \cdot level(lev) \land (lev < 0 \lor lev \gt C) ~\implies\\ \t7 water\_measure\_failed$$

determining when a component failure occurs is also defined in this theory.

Similar constructions work for the pump and pump controller (flow monitor) components. Figure 2 shows the structure of this part of the system. Separate copies of the FailureManager and Transmission theories are included in each of the component theories, but we identify all the different $transmission\_failure$ actions so that a transmission failure in any component generates the same system error event.

  

Figure 2: Construction of Component Theories

SData is also included into each of the theories shown in this diagram.

The theory of the controller then extends the co-limit of the monitor theories with the following attributes and actions:

Types

 
$CState = \{ initialisation, normal, degraded, rescue, emergency\_stop \}$

Constants

 
$hazard\_level(\num): bool$
$min\_level\_estimate(\num,\num): \num$
$max\_level\_estimate(\num,\num): \num$

Attributes

 
cstate: CState

Actions

 
react   $\{ cstate \}$
terminate   $\{ cstate \}$
stop   $\emptyset$
$steam\_boiler\_waiting$    $\emptyset$
$physical\_units\_ready$    $\{ cstate \}$
$program\_ready$    $\emptyset$

Axioms

Some example axioms of the controller are that a terminate event occurs if there have been three successive stop events, or if there has been a transmission error:

$$stop \land \bigcirc{stop} \land \bigcirc\bigcirc{stop} ~\implies~ \bigcirc\bigcirc{terminate}$$

$$transmission\_failure ~\implies~ terminate$$

Given the new mode and water level, take appropriate action:

$$\bigcirc{cstate} = normal ~\lor~ \bigcirc{cstate} = degraded... ...t5 (\bigcirc{water\_quantity} \gt N2 ~\implies~decrease\_flow)$$

$$\bigcirc{cstate} = rescue ~\implies \\ ({min\_level\_estimat... ...tity,steam\_quantity)} \gt N2 ~\implies~\\ \t9 decrease\_flow)$$

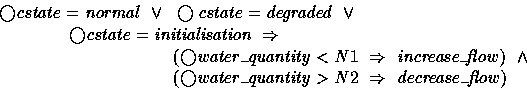
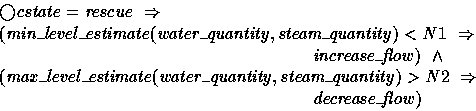
The specification can be validated via animation [11]. The actions $increase\_flow$ and $decrease\_flow$ are general operations which will be interpreted as opening and closing certain pumps in the actual physical system: we have defined a layered architecture in which the implementation details of such abstract actions are hidden from the high-level controller.