Next: 3 Customization of Components Up: 2 Position Previous: 2.1 Component-Based Software
![]()
![]()
![]()
Next: 3 Customization of Components
Up: 2 Position
Previous: 2.1 Component-Based Software
Formal verification requires a formal semantics of the programming language and of the specifications. In this subsection, we give a quick overview of our framework. In particular, we present a formal semantics of class invariants. This semantics reveals the central problems with modular object-oriented programming. The reader may refer to [PH97b,MPH97] for a detailed description of the formal basis.
In the implementation, values of abstract data types are in general represented by several linked objects. We consider such object structures as a whole. Going beyond Larch, the relation between object structures and values of abstract data types is made explicit by so-called abstraction functions (cf. [Hoa72]). Modification of an object X possibly changes the abstractions of all object structures referencing X. As a consequence, the treatment of side-effects becomes very important. The definition of abstraction functions and formal specification of side-effects require a formalization of the data and state model of the programming language. The data model of a programming language defines the objects and values that may be used in programs. The state of an object tells whether the object is allocated, and it assigns an object to each of its attributes. The collection of all object states at a point of program execution is called the current object environment.
For verification, we assume a Hoare-style programming logic (cf. [Hoa69]) as presented in [PH97b]. This logic is a formalization of the axiomatic semantics of the underlying programming language. Thus, correctness of a program is showed by translating its specification into Hoare triples and proving these triples in the logic.
Certainly, invariants need not hold in all intermediate
states during execution of C's methods; in particular
during the construction of linked object structures,
invariants are usually violated. We require invariance only for public methods,
because this guarantees that the invariant of a class C holds outside
the execution of methods of C and because we want to
allow private methods to perform auxiliary operations
violating, e.g., well-formedness properties.
To use class invariants as invariants in the proof
technical sense, they have (a) to be true in possible initial program states
and they have (b) to be invariant under all public methods.
Requirement (a)
is trivially satisfied because no user-defined objects are allocated in
initial program states. Requirement (b) is the proof obligation resulting
from invariants. Although requirement (b) is as well
justified from an operational point of view -- a method mC of class C
can call a method mD of class D and thus manipulate D-objects --,
the literature often assigns a weaker meaning to invariants
which makes verification much more difficult and leads to unintuitive
situations.![[*]](foot_motif.gif)
We define the formal semantics of specifications by interpreting them as
triples in a Hoare-style logic.
Thus, the connection between specifications and programs is precisely
defined. Let us assume
a program P with classes ![]() . The specification
of P consists of the class invariants
. The specification
of P consists of the class invariants ![]() and
of a pre-postcondition-pair (Pm,Qm) for each method m.
To verify P, we have to prove a triple of the following form for each
public method m, where $ denotes the current object environment:
and
of a pre-postcondition-pair (Pm,Qm) for each method m.
To verify P, we have to prove a triple of the following form for each
public method m, where $ denotes the current object environment:
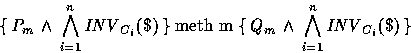
Peter Mueller and Arnd Poetzsch-Heffter